1553. Прыгун по платформам

В старой аркадной игре Вы попали на бонусный уровень. Имеется набор платформ, на которых находятся монеты. Вы должны прыгать с одной платформы на другую, собирая деньги. С каждой платформы можно прыгать только на платформу, находящуюся ниже. Начальной можно выбрать любую платформу.

Опишем поведение игрока при прыжках. При каждом прыжке горизонтальная составляющая скорости является константой, не превышающей v. Движение вниз происходит по законам физики: ускорение свободного падения равно g. Начальная скорость игрока равна 0.

Каждая платформа является точкой и имеет формат “X Y C”, где X и Y – координаты платформы, а C – количество монет на ней. Большие значения координаты Y имеют платформы, находящиеся выше. Определить наибольшее количество монет, которое может собрать игрок.

Вход. Состоит из нескольких тестов. Первая строка каждого теста содержит три целых числа: количество платформ n (1 ≤ n ≤ 50), а также значения v и g (1 ≤ v, g ≤ 100). Следующие n строк описывают платформы в формате "X Y C". Известно, что 0 ≤ X, Y ≤ 5000, 0 ≤ C ≤ 10000.

Выход. Для каждого теста вывести в отдельной строке наибольшее количество монет, которое может собрать игрок.

Пример входа	Пример выхода
3 2 10 3 10 7 5 15 7 8 9 12 3 1 2 0 0 1 2 4 1 4 0 1	14 2

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Поскольку игрок при прыжках всегда движется вниз, то его путь всегда конечный, а каждая платформа может быть посещена не более одного раза. Пусть opt[i] содержит наибольшее количество монет, которое можно собрать по всем путям, заканчивающихся на i - ой платформе. Обозначим через s[i] множество платформ, с каждой из которых за один прыжок можно попасть на i - ую платформу. Пусть coins[i] – количество монет, находящихся на i - ой платформе. Тогда имеет место рекуррентность:

opt[i] = coins[i] +

Остается научиться определять, можно ли прыгнуть из одной платформы на другую. Пусть платформы имеют координаты (x₁, y₁) и (x₂, y₂), y₁ > y₂. Игрок должен преодолеть по горизонтали расстояние |x₁ – x₂|, по вертикали |y₁ – y₂|. Наибольшая горизонтальная скорость движения при прыжке равна v, которая по условию задачи постоянна. Тогда время, за которое может быть преодолена горизонтальная составляющая, равно t = |x₁ – x₂| / v. Вычислим расстояние, на которое переместится за это время игрок по оси ординат. Оно равно

dy = g * t² / 2

Если dy > |y₁ – y₂|, то прыжок совершить невозможно. Перепишем последнее неравенство в виде:

g * |x₁ – x₂|² / 2v² > |y₁ – y₂|,

или для избежания операции деления:

g * |x₁ – x₂|² > |y₁ – y₂| * 2v²

Отсортируем платформы по y - координате. Последовательно, начиная с наивысшей платформы, вычисляем значения массива opt согласно выше приведенной рекуррентной формуле. В переменной res накапливаем ответ – он равен наибольшему значений среди всех ячеек массива opt.

Пример

Рассмотрим следующий тест:

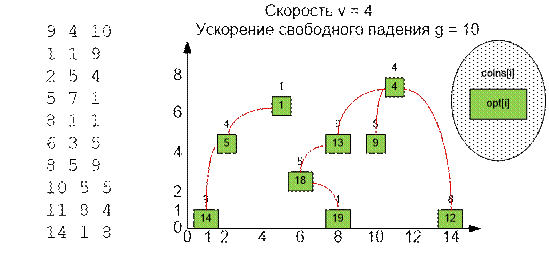
Наибольшее количество монет, которое может собрать игрок, равно 19. Путь игрока начинается на платформе с координатами (11, 8) и заканчивается на платформе с координатами (8, 1).

Реализация алгоритма

Информацию о платформе храним в структуре pos, которая содержит ее координаты (x, y) и количество монет coins на ней.

struct pos

{

long long x, y, coins;

} c[50];

Функция сортировки – платформы сортируются по возрастанию y - координат.

int f(pos a, pos b)

{

return a.y < b.y;

}

Начиная с последней платформы (наивысшей, которая имеет наибольшую y - координату), вычисляем значения ячеек opt[i].

int maxCoins(int v, int g)

{

int i, j, res = 0;

for(i = n - 1; i >= 0; i--)

{

Если мы начинаем сбор монет с i-ой платформы и в ней же сбор заканчиваем, то положим opt[i] = c[i].coins.

opt[i] = c[i].coins;

for(j = i + 1; j < n; j++)

Если с j-ой платформы можно прыгнуть на i-ую платформу (i < j), и при этом сумма opt[j] + c[i].coins будет больше opt[i], то пересчитываем значение opt[i].

if ((opt[j] + c[i].coins > opt[i]) &&

(g * (c[i].x - c[j].x) * (c[i].x - c[j].x) <=

(c[j].y - c[i].y) * 2 * v * v))

opt[i] = opt[j] + c[i].coins;

if (opt[i] > res) res = opt[i];

}

return res;

}

Основная часть программы. После считывания входнх данных сортируем платформы по возрастанию их ординат. Вычисляем и выводим результат.

while(scanf("%d %d %d",&n,&v,&g) == 3)

{

for(i = 0; i < n; i++)

scanf("%lld %lld %lld",&c[i].x,&c[i].y,&c[i].coins);

sort(c,c+n,f);

res = maxCoins(v,g);

printf("%d\n",res);

}